SciPy.optimize:解の求め方と最適化問題#
import numpy as np
import scipy.optimize as op
import pandas as pd
# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")
はじめに#
線形の方程式の解を求めることは比較的簡単である。1変数の場合,式を変形すれば解を簡単に求めることができる。変数が複数ある場合でも,「連立一次方程式の解」の節で説明したように,numpy.linalgを使えば簡単に解を求めることができる。例えば,差分方程式と経済分析で扱う45度線モデルと蜘蛛の巣モデルは線形であるため、長期的な均衡の値を簡単に計算することができる。またソロー・モデルも線形ではないが、定常状態の資本ストック(\(k_*\))について解くことができるので、長期的な値を計算することが可能である。しかし非線形モデルによっては、長期的均衡の値を簡単に求めることができない場合もあり、その場合に使う手法をここで説明する。
コードを書いて非線形の方程式の解を求めるには色々な方法があるり,ここではその代表的な方法の考え方についてまず説明する。その後SciPy(「サイパイ」と読み,Scientific Pythonの略)というパッケージにあるoptimizeというモジュールを紹介する。SciPyはNumPyの大幅な拡張版と理解して良いだろう。SciPyを読み込むとNumPyの関数などを利用できるようになる。しかしSciPyは大きなパッケージであり,全てを読み込む必要もない。従って,NumPyを読み込んでSciPyのサブパッケージや関数を読み込むということで十分であろう。そしてSciPyのモジュールoptimizeに非線形の方程式の解を簡単に求めることができる関数が含まれている。もちろんこれらの関数は線形の方程式の解を求める為にも使える。またscipy.optimizeには最適化問題のための関数も用意されており,Pythonで経済学を学ぶ為には必須となるツールと言えるだろう。消費者の効用最大化問題やソロー・モデルの資本の黄金律水準などに応用して使い方を説明する。
解の求め方と考え方#
Bisection法#
説明#
Bisection法の考え方について説明するために,次の関数を考えよう。
def f(x):
return x**3 + 4*x**2 -3
次に3つの変数a,b,cに下の値を割り当てる。
a = -3.0
b = -0.5
c = 0.5*(a+b)
\(x\)がa,b,cの値を取る場合の\(f(x)\)の値を計算してみよう。
f(a), f(b), f(c)
(6.0, -2.125, 3.890625)
これらの情報を図示すると次のようになる。
x = np.linspace(-3.1, 0, 100) # 1
df1 = pd.DataFrame({'X':x, 'Y':f(x)}) # 2
ax = df1.plot('X','Y') # 3
ax.axhline(0, c='orange') # 4
ax.text(a,-1,"a") # 5
ax.text(b,-1,"b")
ax.text(c,-1,"c")
ax.scatter([a,b,c], [f(a), f(b),f(c)], s=50, c='k') # 6
ax.scatter([a,b,c], [0,0,0], s=50, c='red')
pass
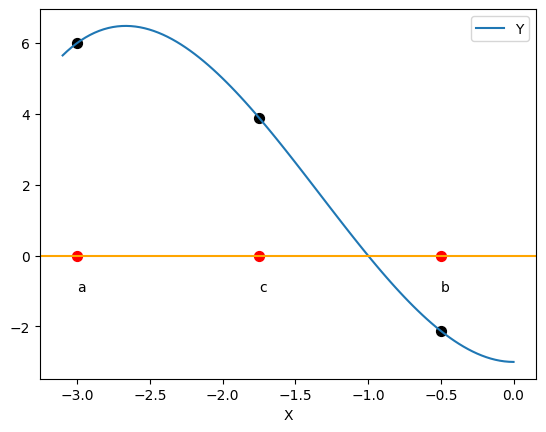
コードの説明
-3.1から0から等間隔で100の値を生成し横軸に設定する。xとf(x)の値からなるDataFrameの作成。Xを横軸、Yを縦軸に指定しf(x)の曲線をプロットする。また図の軸をaxとする。axのメソッドaxhline(<横軸の値>)を使いaxに平行線を表示する。c='orange'は色を指定する引数。axのメソッドtext(<横軸の値>,<縦軸の値>,<表示する文字>)を使いaxに文字を表示する。axのメソッドscatter()を使いaxに点を表示する。第1引数:横軸の値のリスト
第2引数:縦軸の値のリスト
第3引数:点のサイズ
第4引数:点の色
<bisection法の考え方>
中間値の定理に基づく。
f(a)とf(b)の符号が異なりf(x)が連続関数である場合、aとbの間にはf(x)がゼロになるxの値が必ず存在する。(一般的には,f(x)がゼロになるxの値は奇数個存在することになる。)上の図の
c=(a+b)/2はaとbの平均値であり、次の3つの可能性がある。f(c)=0この場合は解が求められたことになる。
f(c)>0(上の図のように)
f(c)とf(a)が同じ符号であるため、次はcとbの間で同様の計算をおこなう。例えば,d=(c+b)/2を計算する。
f(c)<0(上の図とは異なるが)
f(c)とf(a)は異なる符号であるため、次はaとcの間で同様の計算をおこなう。例えば,d=(a+c)/2を計算する。
このように
f(x)=0となるxを「挟み撃ち」するように計算プロセスを続けるとf(x)=0を満たすxの値に十分に近い値を求めることができる。
<注意点>
計算には
aとbのように1つの根を挟む2点が必要となる。挟んだ根だけを求めることになる。
求めた値は近似となる。
求めた値は収束値なので収束する速度が一つの「壁」になり得る。
手計算#
実際にコードを書き,Bisection法の考え理解しよう。次の関数を定義する。
def my_bisect(f,a,b,N):
""" [a,b]におけるf(x)=0の近似解(bisection法) # 1
引数
----------
f : f(x)=0の連続関数
a,b : 根を挟む初期の値
N : 中間値を計算するプロセスの回数
返り値
-------
N回ループ後の解の近似値
* f(a)*f(b) >= 0 の場合、メッセージが返される。
* c=(a+b)/2とし、f(a)、f(b)、f(c)が同じ符号の場合、メッセージが返される。
"""
if f(a)*f(b) >= 0: # 2
print("f(a)とf(b)は同じ符号です。a、bの値を変えてください。")
return None
a_ = a # 3
b_ = b # 4
for n in range(N): # 5
c_ = (a_ + b_)/2 # 6
fc = f(c_) # 7
if f(a_)*fc < 0: # 8
b_ = c_
elif f(b_)*fc < 0: # 9
a_ = c_
elif fc == 0: # 10
print("正確な根が求められました。")
return c_
else: # 11
print("計算に失敗しました。")
return None
print(f'{N}回ループ後の値です。')
return (a_ + b_)/2 # 12
コードの説明
"""と"""で挟んだ領域はdocstringと呼ばれ、関数の説明をする。書かなくても良いが、自分が忘れた頃に関数のコードを読むことになるかもしれないので、書く方がオススメ。f(a)とf(b)の符号が同じ場合は計算を中止する。bisection法では根を挟む2つの変数が必要だが、計算を繰り返す毎に両変数がアップデートされる。そのアップデート用の変数としてa_とb_の初期値をaとbに設定している。(3)を参照。
N回のforループとして中間値を計算する。中間値を計算して変数
c_に割り当てる。中間値での関数の値を変数
fcに割り当てる。中間値と
a_での関数の符号が異なる場合、c_をb_に割り当てる(アップデートする)。(a_は以前と同じ値。)中間値と
b_での関数の符号が異なる場合、c_をa_に割り当てる(アップデートする)。(b_は以前と同じ値。)中間値である
c_での関数の値が0の場合、近似ではなく正確な根が求められることになる。その旨を立てるメッセージを表示し,c_の値を返す。その他の場合は計算の失敗となる。その旨のメッセージを表示し,
Noneを返す。N回のループ終了後にa_とb_の中間値として根の近似値が返される。
次の例を使って実際に計算してみよう。
def f_ex1(x):
return x**2 - 2
f_ex1には次の正と負の2つの解が存在する。
np.sqrt(2), -np.sqrt(2)
(1.4142135623730951, -1.4142135623730951)
まず\(x>0\)の解を計算してみよう。
my_bisect(f_ex1, 0, 2, 10)
10回ループ後の値です。
1.4150390625
次に\(x<0\)の解をしてみる。
my_bisect(f_ex1, -2, 0, 10)
10回ループ後の値です。
-1.4150390625
Nの値が変わると根の近似値がどう変化するか試してみよう。
次の場合は計算に失敗する。
my_bisect(f_ex1, -2, 2, 10)
f(a)とf(b)は同じ符号です。a、bの値を変えてください。
Scipyの関数#
上で考えたmy_bisect()関数は,解法の考えを理解するために使ったが,実際にBisection法を使う場合は,SciPyパッケージのoptimizeモジュールに用意されているbisect()関数を使おう。基本的な考えは同じであり,my_bisect()より格段に洗練された関数と考えれば良いだろう。またBisection法だけではなく他にも様々な方法があり,その一つであるBrent法に基づく関数もここで紹介することにする。
bisect関数#
使い方は、上で定義したmy_bisect関数と基本的に同じであり、近似値が十分に近い数値になるようにforループ回数の引数Nは自動で決定される。
bisect(f, a, b)
f:評価の対象となる関数名a:解探査区間の最小値b:解探査区間の最大値
op.bisect(f_ex1, 0, 2)
1.4142135623715149
op.bisect(f_ex1, -2, 0)
-1.4142135623715149
brentq関数#
brentq関数はBrent法に基づいており、bisect関数を拡張した手法(ここでは説明を割愛)である。より安定的により速く解への収束が可能となっている。基本的に使い方はbisectと同じである。
brentq(f, a, b)
f:評価の対象となる関数名a:解探査区間の最小値b:解探査区間の最大値
op.brentq(f_ex1, 0, 2)
1.4142135623731364
op.brentq(f_ex1, -2, 0)
-1.4142135623730951
bisectとbrentqのどちらを使っても良いが、brentqを使うことを推奨する。
Newton法#
説明#
ここではもう一つの解法であるNewton法について説明する。図にある関数f(x)を考えよう。\(x_1\)での傾きは\(f^{\prime}(x_1)\)であり、次の式が成り立つことが確認できる。

Fig. 3 Newton法#
即ち、\(x_0\)が与えられ\(f^{\prime}(x_0)\)が分かれば、\(x_1\)を求めることができる。更に、\(x_1\)が与えられ、\(f^{\prime}(x_1)\)が分かれば、\(x_2\)を求めることができる。一般的には次の差分方程式が成り立つことになる。
この式に従って\(x_{t+1}\)の計算を続けると、\(x_{t+1}\)は\(f(x)=0\)を満たす\(x\)に漸近的に近づいていき、根に十分に近い値を計算することが可能となる。
<コメント>
求めた値は近似となる。
bisec関数とbrentq関数よりも早い率で解に収束する特徴がある。bisec関数とbrentq関数と違って、必ず解を求めることができるとは限らない。解探索のxの初期値の設定が重要となる。
手計算#
Newton法の基本的な考えを説明するために式Newton法を捉える関数を定義しよう。
def my_newton(f,Df,x0,N):
""" Newton法でf(x)=0の根を近似する。
引数
----------
f : f(x)=0の関数名f
Df : f(x)の導関数
x0 : 解探索の初期のxの値
N : ループの回数
返り値
-------
根の近似値
Df(x) == 0の場合は None がメッセージが表示される。
"""
x_ = x0 # 1
for n in range(N): # 2
fx = f(x_) # 3
Dfx = Df(x_) # 4
if Dfx == 0: # 5
print('導関数はゼロです。解は見つかりませんでした')
return None
else: # 6
x_ = x_ - fx/Dfx
print(f'{N}回ループ後の値です。')
return x_ # 7
コードの説明
例としてf_ex(x)を使うが、まず導関数を定義する。
def Df_ex1(x):
return 2*x
まず\(x>0\)の解を求めよう。
my_newton(f_ex1, Df_ex1, 1, 10)
10回ループ後の値です。
1.414213562373095
次に\(x<0\)の解を求める。
my_newton(f_ex1, Df_ex1, -1, 10)
10回ループ後の値です。
-1.414213562373095
次は計算に失敗するケースとなる。
my_newton(f_ex1, Df_ex1, 0, 10)
導関数はゼロです。解は見つかりませんでした
Scipyの関数#
Scipyパッケージのoptimizeモジュールにはnewton法の関数が用意されており、説明で使った手計算のmy_newton()関数と比べると格段に洗練れている。使い方は簡単で、引数に関数とxの初期値を指定するだけであり、近似の誤差とループの回数は自動的に設定される。
newton(f, x0)
f:評価の対象となる関数名x0:解探査の初期値
op.newton(f_ex1, 1)
1.414213562373095
op.newton(f_ex1, -1)
-1.414213562373095
またリストとしてxの初期値を複数設定することも可能である。
op.newton(f_ex1, [1,10])
array([1.41421356, 1.41421356])
これを利用して、複数の根を同時に計算することも可能となる。
op.newton(f_ex1, [-1,1])
array([-1.41421356, 1.41421356])
マクロ経済学への応用#
45度線モデル#
ケインズの45度線モデルでは,所得\(Y\)以外の変数は外生変数として所得が決定されるマクロ経済学の基本的なモデルである。次の記号・仮定を使う。
所得:\(Y\)
計画支出:\(E=C(Y)+I+G\)
消費関数:\(C(Y)=d+cY^{a}\)
自発的消費:\(d=10\)
限界消費性向:\(c=0.7\)
\(\alpha=0.7\)
投資:\(I=15\)
政府支出:\(G=10\)
均衡:\(E=Y\)
1つの式でまとめると次式となる。
この式をプロットするために,次のパラメータの下でのh0()関数を定義する。
a = 0.5
c = 0.7
d = 10
i = 15
g = 10
def h0(y):
a = 0.8
c = 0.7
d = 10
i = 15
g = 10
return y - (i + g + d + c*y**a)
プロットしてみよう。
yy = np.linspace(20,100,100)
df1 = pd.DataFrame({'Y':yy, 'h0(Y)':h0(yy)})
ax_ = df1.plot('Y','h0(Y)')
ax_.axhline(0,c='red')
pass
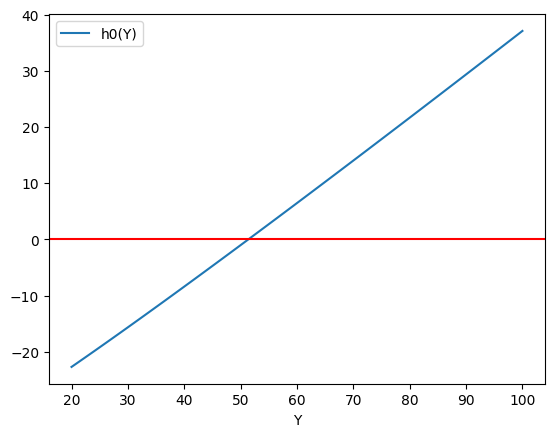
h0(y)関数は右上りとなっている。傾きを直感的に説明すると次のようになる。Yが増加すると,当たり前だが所得Yは線形的に増加する。一方で,計画支出の一部である消費も増加するが,aは0.5に設定されているため,増加分は逓減している。したがって,所得と計画支出の差は上昇することになる。
均衡の\(Y\)を計算してみよう。
<Bisection法>
op.bisect(h0, 40, 60)
51.35063858666513
<Brent法>
op.brentq(h0, 40, 60)
51.35063858666476
<Newton法>
op.newton(h0, 40)
51.35063858666476
IS曲線の導出#
ここでも45度線モデルを使い財市場の均衡で決定される所得\(Y\)を考えるが,投資は利子率\(r\)の非線形の減少関数と仮定する。この仮定により,利子率\(r\)を所与とした所得の均衡を考えることが可能となり,非線形の\(IS\)曲線をプロットすることができる。
45度線モデルの投資\(I\)を次のように変更する。
\(r=\) 実質利子率
\(j=15\)
\(b=0.5\)
均衡式は次式で与えられる。
まず関数を再定義するが,\(y\)と\(r\)を引数とする。
def h1(y,r):
a = 0.8
b = 0.5
c = 0.7
d = 10
i = 15
j = 15
g = 10
return y - ( j/r**b + i + g + d + c*y**a )
\(r\)の複数の値を設定する。
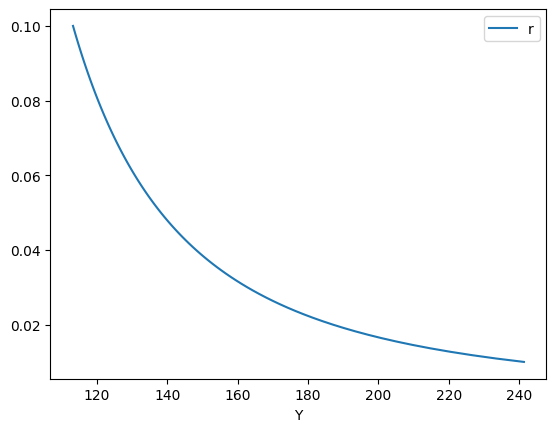
r_arr = np.linspace(0.01, 0.1, 100)
次にforループを使い、財市場での均衡が成立するrとYの組み合わせを計算する。
y_list = []
for r in r_arr:
y = op.newton(h1, 30, args=(r,)) # 1
y_list.append(y)
df2 = pd.DataFrame({'Y':y_list, 'r':r_arr})
コードの説明
関数
h1(y,r)にはyとrの2つの引数がある。一方、関数newton()ではh1()の第一引数の値を計算することを想定しており,「その他の引数」はargsで指定する必要がある。この機能を利用することにより、rを所与としてh1(y,r)=0となるyの値を計算することが可能となる。argsを指定する際、タプル()で「その他の引数」を指定し、それが1つの場合は(r,)のように,を付け加える必要がある(基本的にタプルは,で定義されるため)。
df2.plot('Y','r')
pass
ソロー・モデル#
モデルの簡単な説明は「ソロー・モデル」の章を参照してほしい。
産出量:\(y_t\)
資本ストック:\(k_t\)
労働:\(l_t=1\)(労働人口増加率は
0)貯蓄率:\(0<s<1\)
資本減耗率:\(0<d<1\)
生産性:\(A>0\)
生産関数:\(y_t=Ak_t^a\)
資本の蓄積方程式:
\[ k_{t+1} = sAk_t^a + (1-d)k_t \]定常状態での\(k_t\):\(k_*\)
\[ 0 = sAk_*^a + (1-d)k_* - k_* \equiv m(k_*) \]
パラメターを次の値とする
s = 0.2
a = 0.3
d = 0.1
A = 10
\(k\)の定常状態\(k_*\)は次式で定義される。
この方程式の解を求めるが,関数kss()を定義しよう。
def kss(k):
return s*A*k**a + (1-d)*k - k
まず式(2)をプロットするが,そのために\(k\)の値を設定しよう。
k_arr = np.linspace(0,100, 1000)
forループでkss(k_*)を計算し、結果をDataFrameに格納する。
k_list = []
for k in k_arr:
k_list.append(kss(k))
df3 = pd.DataFrame({'k':k_arr, 'kss(k)':k_list})
ax_ = df3.plot('k', 'kss(k)')
ax_.axhline(0, c='red')
pass
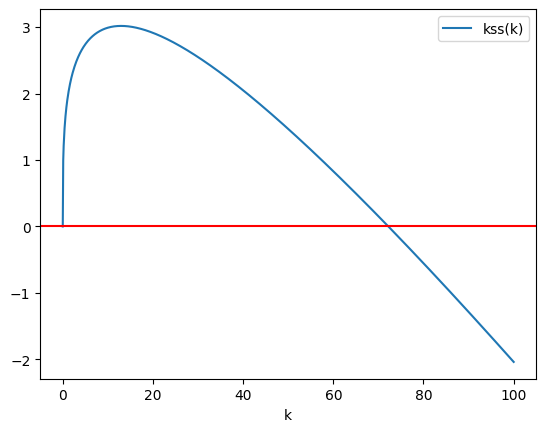
scipy.optimizeを使い定常状態\(k_*\)を計算してみよう。
<Bisection法>
op.bisect(kss, 60, 100)
72.21281575281978
<Brent法>
op.brentq(kss, 60, 100)
72.21281575282009
<Newton法>
op.newton(kss, 60)
72.21281575281984
投資#
企業の投資問題を考える。初期投資fcを投入すると\(T\)期間\(\pi\)の利潤を得るとする。実質利子率は\(r\)とすると\(T\)期間の利潤の現在価値の合計は次のようになる。
パラメータは次の値としよう
r = 0.07
pi = 10
fc = 100
問題:
「投資の正味現在価値(net present value)がゼロになるにはどれだけ長く事業が続く必要があるか?」
利潤の正味現在価値は
で与えられる。この式を捉える関数を作成しよう。
def npv(x):
return (1-np.exp(-x*r))*pi/r - fc
Newton法を使いnpv()がゼロになる\(T\)を計算する。
op.newton(npv,10)
17.19961149037052
最適化問題:1変数の場合#
説明#
最適化問題は経済学の根幹をなすが、ここではscipy.optimizeのminimize_scalar関数の使い方を簡単に説明する。様々な引数が用意されているが、基本的には次のようなコードの書き方となる。
デフォルトではBrent法が使われる。
minimize_scalar(f, bracket=(a,b))
fは最小化したい関数名bracketは計算の初期値を指定する引数であり、省略可能。初期値を設定する場合は2つ必要である。関数を最小化すると思われるxに対して必ずしもa<x<bが満たされるようにaとbの値を設定する必要はなく、下で定義するf_ex2の例が示すように、必ずしも区間内に解があるとは限らない。
Bounded法を使う場合
minimize_scalar(f, method='bounded', bounds=(a,b))
f:最小化したい関数名method:計算手法を指定する引数であり、boundedを指定する(デフォルトはbrent)。boundsは関数を最大化するxの値を探す区間を指定する引数であり、aは区間の最小値、bは区間の最大値(裏でBrent法が使われており、関数を最小化するxの探索はboundsで指定した区間に限られる)
<2つの注意点>
返り値は、関数を最小化する変数の値だけではなく、様々な情報が整理されたオブジェクトとして返される。
最大化のための関数は用意されていない。従って、最大化したい関数にマイナスの符号をつけて
minimize_scalar()関数を評価する必要がある。
例1#
f_ex1関数を例として考えよう。最小化されるxを計算する。
res1 = op.minimize_scalar(f_ex1)
res1
message:
Optimization terminated successfully;
The returned value satisfies the termination criteria
(using xtol = 1.48e-08 )
success: True
fun: -2.0
x: 9.803862664247969e-09
nit: 36
nfev: 39
この返り値の中で重要なのは次の3つである。
fun(1行目):最小化された場合の関数の値success(最後から2行目):計算が成功したかどうかを示す。True:成功False:失敗
x(最後):関数を最小化する変数の値
それぞれは次のように属性としてアクセスできる。
res1.fun
-2.0
res1.success
True
res1.x
9.803862664247969e-09
例2#
次に最小値が複数ある場合を考えよう。
def f_ex2(x):
return x**4 - x**2
まずこの関数を図示しよう。
xx = np.linspace(-1.1, 1.1, 100)
df_ex2 = pd.DataFrame({'X':xx, 'f_ex2':f_ex2(xx)})
ax_ = df_ex2.plot('X','f_ex2')
ax_.axhline(0,c='red')
pass
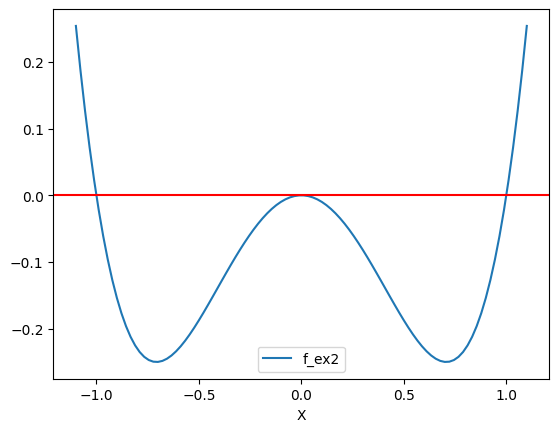
まずmethodのデフォルトであるbrent法を使ってみよう。解が2つあるため、次のコードではPythonが選んだ解しか求めることができない。
res2 = op.minimize_scalar(f_ex2)
res2
message:
Optimization terminated successfully;
The returned value satisfies the termination criteria
(using xtol = 1.48e-08 )
success: True
fun: -0.24999999999999994
x: 0.7071067853059209
nit: 11
nfev: 14
次に引数bracketを使ってみよう。
res3 = op.minimize_scalar(f_ex2, bracket=(-1,-0.5))
res3
message:
Optimization terminated successfully;
The returned value satisfies the termination criteria
(using xtol = 1.48e-08 )
success: True
fun: -0.24999999999999994
x: -0.7071067842613271
nit: 12
nfev: 15
しかし次の2つ例はbracket内に必ず解が存在するとは限らないことを示している。
res3 = op.minimize_scalar(f_ex2, bracket=(-1,-0.8))
res3
message:
Optimization terminated successfully;
The returned value satisfies the termination criteria
(using xtol = 1.48e-08 )
success: True
fun: -0.25
x: -0.7071067804088556
nit: 10
nfev: 13
res3 = op.minimize_scalar(f_ex2, bracket=(-1,-0.1))
res3
message:
Optimization terminated successfully;
The returned value satisfies the termination criteria
(using xtol = 1.48e-08 )
success: True
fun: -0.25
x: 0.7071067805303989
nit: 12
nfev: 15
「ん?」と思うかもしれないが、brentのアルゴリズムがそのようになっているので、その性質を覚えるしかない。
一方、method='bounded'を使うと、boundsで指定された区間の解が探索される。
res4 = op.minimize_scalar(f_ex2, method='bounded', bounds=(-1,0))
res4
message: Solution found.
success: True
status: 0
fun: -0.24999999999998732
x: -0.707106701474177
nit: 10
nfev: 10
ソロー・モデル:黄金律#
資本の黄金律水準とは、長期均衡において一人当たり消費を最大化する資本ストックであり、貯蓄率\(s\)に依存している。それを示すために、まず定常状態の資本ストック\(k_*\)をパラメータで示すが,次式は式(2)から導出できる。
更に、定常状態での一人当たりGDPと消費は次式で与えられる。
これらを使うと、一人当たり消費を貯蓄率の関数として表すことができる。
関数として定義し図示してみよう。
# sの値
s_arr = np.linspace(0,1,100)
# 消費関数
def c(s):
return (1-s)*A*(A*s/d)**(a/(1-a))
# 消費の値を入れるリスト
c_list = []
# 消費の計算
for s in s_arr:
c_list.append(c(s))
# DataFrameの作成
df4 = pd.DataFrame({'s':s_arr, 'c(s)':c_list})
# プロット
df4.plot('s','c(s)')
pass
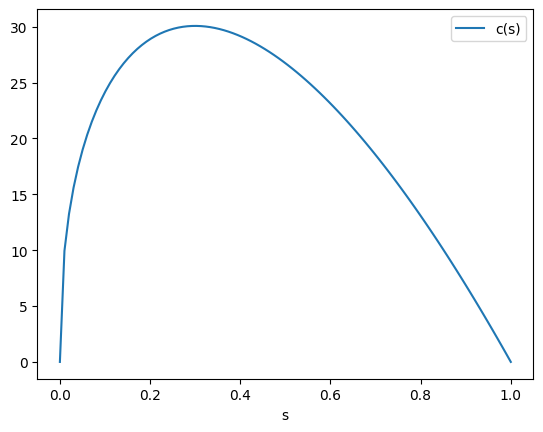
次に一人当たり消費を最大化する貯蓄率を求めるために関数を定義する。
def c_minus(s):
return -(1-s)*A*(A*s/d)**(a/(1-a))
最大化するためにマイナスの符号が追加されていることに留意しよう。
デフォルトのBrent法を使い消費を最大化する貯蓄率\(s\)を求める。
op.minimize_scalar(c_minus)
message:
Optimization terminated successfully;
The returned value satisfies the termination criteria
(using xtol = 1.48e-08 )
success: True
fun: -30.071147877019232
x: 0.30000000024161544
nit: 13
nfev: 16
Bounded法でも同じ解が求められる。
op.minimize_scalar(c_minus, method='bounded', bounds=(0, 1))
message: Solution found.
success: True
status: 0
fun: -30.071147877017722
x: 0.2999998786598638
nit: 9
nfev: 9
労働供給問題#
ミクロ経済学で学ぶ消費者の労働供給問題を考えよう。消費者は消費財と余暇の2財を消費し,効用を最大化する消費財と余暇を選択すると考える。
変数の定義:
\(u\):効用
\(c\):消費
\(l\):労働供給(24時間のパーセント)
\(p\):消費財の価格
\(w\):賃金
\(1\):24時間を100%として。
\(1-l\):余暇
効用関数:
\[u=a\ln(c)+(1-a)\ln(1-l)\]制約式:
(3)#\[pc=wl\]
制約式のもとで消費者は\(c\)と\(l\)を選択し効用を最大化する。
<解法>
制約式を効用関数に代入する
\[\max_{l}\;a\ln\left(\frac{wl}{p}\right)+(1-a)\ln(1-l)\]これにより効用は\(l\)の関数になり,
.minimize_scalar()が使える形になっている。
次の値を仮定する。
a = 0.6
p = 1
w = 10
目的関数(最大化する対象となる関数)を定義する。
def u_minus(l):
return -( a*np.log(w*l/p)+(1-a)*np.log(1-l) )
効用を最大化する。
res_u = op.minimize_scalar(u_minus, method='bounded', bounds=(0,1))
res_u
message: Solution found.
success: True
status: 0
fun: -0.7085393887825051
x: 0.5999985035112788
nit: 9
nfev: 9
print(f'最適な労働供給は{res_u.x:.2f}である。')
最適な労働供給は0.60である。
予算制約式から消費量は
となるので,
print(f'最適な消費量は{res_u.x*w/p:.2f}である。')
最適な消費量は6.00である。
print(f'最大化された効用水準は{-res_u.fun:.2f}である。')
最大化された効用水準は0.71である。
結果を図示するために、効用関数を\(c\)で解くと次式となる。
この関数を捉える関数を作成しよう。
def c_utility(l):
return ( np.exp(-res_u.fun)/(1-l)**(1-a) )**(1/a)
プロットするために図の横軸になる労働供給\(l\)の値を生成する。
l_arr = np.linspace(0,0.999,100)
(注意)次のコードで\(l=1\)になると警告が出てしまう。理由は式(5)の右辺の分母がゼロになるためである。それを避けるために,0から0.999の間の値を100個生成している。
これらを使い、無差別曲線の値を計算する。この際、res_u.funを利用する(マイナスになることに注意しよう)。
c_utility_list = []
for l in l_arr:
c_utility_list.append(c_utility(l))
次に制約線の値を生成する。
c_constraint_list = []
for l in l_arr:
c_constraint_list.append(w*l/p)
ここで式(4)を使っている。
値をDataFrameにまとめる。
df_5 = pd.DataFrame({'l':l_arr,
'c_utility':c_utility_list,
'c_constraint':c_constraint_list})
df_5を使いプロットする。
ax_ = df_5.plot('l','c_utility') # 1
df_5.plot('l','c_constraint', ax=ax_) # 2
ax_.set_ylim([0,20]) # 3
pass
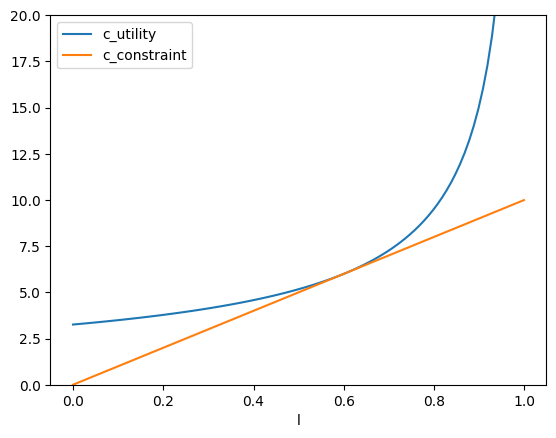
コードの説明
プロットの軸を
ax_に割り当てている。制約式のずを同じ軸に表示するために引数
ax=ax_を使い、軸をax_に指定している。set_ylim()は軸ax_のメソッドであり、縦軸の表示範囲を指定する。
最適化問題:2変数の場合#
説明#
2変数の場合はminimize関数を使う。様々な引数が用意されているが、基本的には次のようなコードの書き方となる。
minimize(f, x0, bounds=(a,b), constraints)
fは最小化したい関数名f(x)のように引数はx1つで書く必要があり、xをarrayと理解すれば良いだろう(例を参照)。
bounds(指定しなくても良い)は関数を最大化するxの値を探す区間を指定する引数である。aは区間の最小値、bは区間の最大値を指し、次のように設定する。[(変数1の最小値, 変数1の最大値), (変数2の最小値, 変数2の最大値)]
指定しない箇所は
Noneとする。例えば、非負の値に限定したい場合は[(0,None),(0,None)]とする。裏でBrent法が使われており、関数を最小化する
xの探索はboundsで指定した区間に限られる。
constraints(指定しなくても良い)は制約式。1つの制約式を1つの辞書として設定する。また制約式が複数ある場合は、それぞれに辞書を作成し、複数の辞書からなるリストもしくはタプルとして設定する。
詳細は例3と例4を参照
<2つの注意点>
返り値は、関数を最小化るる変数の値だけではなく、様々な情報が整理されたオブジェクトとして返される。
最大化のための関数は用意されていない。従って、最大化した関数にマイナスの符号をつけて
minimize()関数を評価する必要がある。
例1#
次の最小化問題を考えよう。
まず関数を定義するが、次の点に留意すること。
f_ex3の引数xをarrayとして考える。xの第0要素をyとし、第1要素をzとする。次のようなイメージ
x = np.array(y,z)
def f_ex3(x): # 1
y = x[0] # 2
z = x[1] # 3
return y**2 + y*z + z**2 + 10 # 4
コードの説明
関数
f_ex3の引数xをarrayと想定する。xの第0要素をyに割り当てる。xの第1要素をzに割り当てる。最大化する関数を返す。
次に解探索の初期値を設定しよう。
x0 = [0.3, 0.5]
x0の第0要素はyの初期値、第1要素はzの初期値となる。これは関数f_ex3の引数であるxの要素の順番に対応している。
res3 = op.minimize(f_ex3, x0=x0)
res3
message: Optimization terminated successfully.
success: True
status: 0
fun: 10.000000000001792
x: [-1.260e-06 1.406e-06]
nit: 3
jac: [-1.073e-06 1.550e-06]
hess_inv: [[ 6.687e-01 -3.356e-01]
[-3.356e-01 6.691e-01]]
nfev: 12
njev: 4
この返り値の中で重要なのは次の4つである。
fun(1行目):最小化された場合の関数の値message(5行目):「最適化は成功した」というメッセージsuccess(最後から2行目):計算が成功したかどうかを示すブール値。True:計算成功False:計算失敗
x(最後):関数を最小化する変数の値第0要素は
yの値、第1要素はzの値
それぞれは次のように属性としてアクセスできる。
res3.fun
10.000000000001792
res3.message
'Optimization terminated successfully.'
res3.success
True
res3.x
array([-1.26041337e-06, 1.40562889e-06])
例2#
次の最大化問題を考えよう。
まず関数を定義するが,例1と同様に次の点に要注意。
f_ex4の引数xはarrayとして考える。xの第0要素をyとし、第1要素をzとする。次のようなイメージ
x = np.array(y,z)
返り値にマイナスの符号が追加されている。
def f_ex4(x):
y = x[0]
z = x[1]
return -( -z**2-y**2+z*y+z+y )
次に解探索の初期値を設定する。
x0 = [0.5, 0.5]
解探索の初期値として[0.5, 0.5]を設定し計算する。
res4 = op.minimize(f_ex4, x0=[0.5, 0.5])
res4
message: Optimization terminated successfully.
success: True
status: 0
fun: -0.9999999999999998
x: [ 1.000e+00 1.000e+00]
nit: 1
jac: [ 0.000e+00 0.000e+00]
hess_inv: [[1 0]
[0 1]]
nfev: 6
njev: 2
例3#
ここでは制約付き最大化問題を考える。次の制約のもとで例2のf_ex4を最大化するとしよう。
制約式の導入を4つのステップに分けて説明する。
<ステップ1>
制約式を捉えるコード書くために、左辺が非負となるように書き換える。
<ステップ2>
この式の左辺が返り値となる関数を定義する。
def f_const(x):
y = x[0]
z = x[1]
return x[0]+x[1]-1
ここでも引数xはarrayと想定しており,第0要素をyに,第1要素をzに割り当てている。
<ステップ3>
この関数を使い次のように引数constraintsに設定する変数を作成する。
const = {'type':'eq', 'fun': f_const}
右辺は辞書となっており、キーと値の2つのペアがある。
type:制約式のタイプを指定するキー。eq:制約式が等号の場合。ineq:制約式が不等号の場合。
fun:制約式を指定するキー。f_const:制約式の関数名
<ステップ4>
引数constraintsに変数constを指定し計算する(初期値を[5.0, 0.6]とする)。
res5 = op.minimize(f_ex4, x0=[5.0, 0.6], constraints=const)
res5
message: Optimization terminated successfully
success: True
status: 0
fun: -0.7499999999999014
x: [ 5.000e-01 5.000e-01]
nit: 4
jac: [-5.000e-01 -5.000e-01]
nfev: 13
njev: 4
multipliers: [-5.000e-01]
print(f'yは{res5.x[0]:.1f}であり、zは{res5.x[1]:.1f}です。')
yは0.5であり、zは0.5です。
yの値とzの値は制約式を満たすことがわかる。また制約式がない場合と比べて、yの値とzの値は異なり、最大化された関数の値も異なる。
print(f'制約式がない場合の関数の最大値は{-res4.fun:.2f}であり、制約がある場合は{-res5.fun:.2f}となる。')
制約式がない場合の関数の最大値は1.00であり、制約がある場合は0.75となる。
例4#
制約が不等式の場合を簡単に説明する。例3の制約式を
としよう。
<ステップ1>
左辺が非負になるように書き換えると
となる。
<ステップ2>
この不等式の左辺を制約式としてコードを書くが、上のf_constと異なることがわかる。
def f_const_ineq(x):
y = x[0]
z = x[1]
return 1-x[0]-x[1]
<ステップ3>
この場合の引数constraintに使う辞書は次のようになる。
const_ineq = {'type':'ineq', 'fun': f_const_ineq}
constとの違いは、キーtypeに対応する値がineqになっており、funにはf_const_ineqが指定されている。
<ステップ4>
計算すると同じ結果になることが確認できる。
op.minimize(f_ex4, x0=[5.0, 0.6], constraints=const_ineq)
message: Optimization terminated successfully
success: True
status: 0
fun: -0.7499999999999029
x: [ 5.000e-01 5.000e-01]
nit: 4
jac: [-5.000e-01 -5.000e-01]
nfev: 13
njev: 4
multipliers: [ 5.000e-01]
当たり前だが例3の解と同じになっている。
労働供給問題#
労働供給問題を再考する。まず効用関数を設定し直そう。
def u(x):
c = x[0]
l = x[1]
return -( a*np.log(c)+(1-a)*np.log(1-l) )
次に制約式(3)だが、下のように書き換えることができる。
これを使い制約式を定義する。
def budget(x):
c = x[0]
l = x[1]
return w*x[1]-p*x[0]
引数constraintに使う辞書は次のように書くことができる。
const = {'type':'eq', 'fun': budget}
また経済理論から次のことが明らかである。
cは非負lは0と1の間にある
この情報を引数boundsに設定するが、次のような書き方となる。
[(cの最小値、cの最大値), (lの最小値、lの最大値)]
ここでcとlの順番は関数budgetの引数xに対応しており,それぞれの要素の値は
cの最小値:0cの最大値:\(w/p\)lの最小値:0lの最大値:1
となる。これらの値を使い引数boundsに設定する値を次のようにする。
bnds = [(0,w/p),(0,1)]
# 初期値
x0 = [4.0, 0.3]
# 計算
op.minimize(u, x0, bounds=bnds, constraints=const)
message: Optimization terminated successfully
success: True
status: 0
fun: -0.7085392478810801
x: [ 6.003e+00 6.003e-01]
nit: 6
jac: [-9.996e-02 1.001e+00]
nfev: 18
njev: 6
multipliers: [ 1.000e-01]
minimize_scalar()で解いた値と同じであることが確認できる。
練習問題#
予算制約式が不等号の場合の労働供給問題を解きなさい。

