Numpy: ランダム変数

`Numpy`: ランダム変数#

in English or the language of your choice.

import japanize_matplotlib
import numpy as np
import pandas as pd

# 警告メッセージを非表示
import warnings
warnings.filterwarnings("ignore")

はじめに#

1日の生活はランダムな事象の連続と考えることができる。今朝，目覚ましがなったかもしれないが，事後的に考えると，壊れて音が鳴らずに授業に遅刻する確率は全くの0では無かったはずだ。家を出て駅に向かって歩いていると急に雨が降って来るかもしれない。これも大気の状態によって確率的に起こっていると考えることができる。生活する上で，このようなランダムな事象について特に意識しないかもしれないが，毎日がその連続と考えることができる。同様に，個々の企業もランダムな事象に直面している（例えば，ライバル企業の新たな商品・サービスの発表）。また，株式市場を見れば分かるように，需要者と供給者からなる市場の均衡もそうである。更には，日本経済全体では大小様々なランダムな事象が発生していると考えることができる。大きなランダムな事象の例としては，極端な緩和政策を取り続ける日本銀行が急に金融引き締めに動くことが挙げられる。もしくは，急に（可能性は囁かれていた）ロシアがウクライナを侵略することによりインフレが発生し，景気後退の引き金になったのも確率的な事象と捉えることができる。即ち，経済を考える上で，ランダムな事象は無視できない要素だということであ。

このような問題意識に基づき，本章の目的はNumPyを使ったランダム変数の生成方法について簡単に解説することである。

ランダム変数生成コード#

NumPyのrandomモジュールを使いランダム変数を生成するが，randomモジュールの中でまず最初に使う必要があるのがdefault_rng()関数である。以下では続くコードを分かりやすくするためにdefault_rng()を変数rngに割り当てる。

rng = np.random.default_rng()

rngはrandom number generatorの略であり，様々なランダム変数のための下準備となる。言い換えると，rngはランダム変数を生成するための「種」であり，この「種」に分布関数を指定することによりランダム変数が生成される。以下では正規分布と一様分布の使い方を例に説明する。

Tip

ランダム変数の生成にはパッケージSciPyのstatsモジュールを使うこともできる。興味がある人はこのリンクを参照しよう。

正規分布#

正規分布に従うランダム変数の生成方法につて説明する。

コード

rng.normal(loc=0, scale=1, size=1)

loc：平均（デフォルトは0）
scale：標準偏差（デフォルトは1）
size：ランダム変数の数（デフォルトは1）

ここで、.normal()はrngのメソッドである。例として、平均5，標準偏差2の標準正規分布から10のランダム変数を生成しよう。

rng.normal(5, 2, 10)

array([4.47137984, 2.52681009, 4.81914283, 7.40406306, 5.60609614,
       8.30912693, 8.44837751, 3.95471307, 4.54987864, 4.08141801])

上のコードを実行する度に値が変化することが確認できるはずだ。

標準正規分布から5のランダム変数を生成する場合はlocとscaleを省略する。ただし２つ以上のランダム変数を生成する場合はキーワード引数size=が必ず必要となる。

rng.normal(size=5)

array([ 0.71781219, -0.66048976,  2.14425684, -0.27834236,  0.11929538])

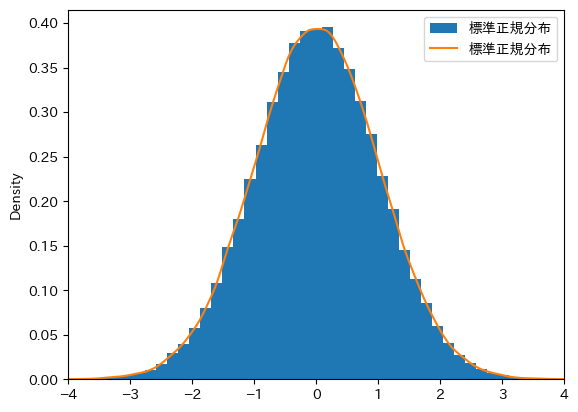
標準正規分布に従う100,000個のランダムを生成しヒストグラムをカーネル密度制定をプロットしてみよう。

# ランダム変数のDatFrame
df_norm = pd.DataFrame({'標準正規分布':rng.normal(size=100_000)})

# ヒストグラム
ax_ = df_norm.plot(kind='hist', bins=50, density=True)

# カーネル密度関数
df_norm.plot(kind='density',ax=ax_)

# 横軸の表示幅の設定
ax_.set_xlim(-4,4)
pass

_images/6915be793801e207cf43d26dfdfc4808cb815dde9eb1d840396bc2687c2fab92.png

一様分布#

一様分布に従うランダム変数の生成方法につて考える。

コード

rng.uniform(low=0, high=1, size=1)

low：最小値（デフォルト0）
high：最大値（デフォルト1）
size：ランダム変数の数（デフォルト1）

.uniform()もrngのメソッドである。最小値5，最大値30の一様分布から10のランダム変数を生成してみよう。

rng.uniform(5, 30, 10)

array([13.71465504, 25.26792365, 11.46227746, 26.08447047,  5.97852205,
       28.51027214, 26.68873283, 27.74691017, 25.03399816, 15.73894502])

最小値0，最大値1の一様分布から5のランダム変数を生成する。

rng.uniform(size=5)

array([0.17783045, 0.7518265 , 0.8171626 , 0.65557511, 0.65979815])

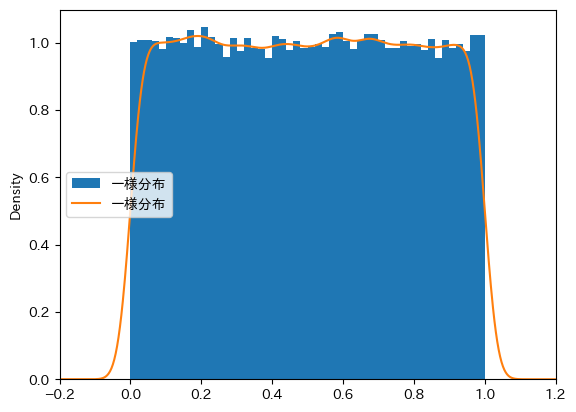
\([0,1]\)の一様分布に従う100,000個のランダムを生成しヒストグラムをカーネル密度制定をプロットしてみよう。

# ランダム変数のDatFrame
df_uni = pd.DataFrame({'一様分布':rng.uniform(size=100_000)})

# ヒストグラム
ax_ = df_uni.plot(kind='hist', bins=50, density=True)

# カーネル密度関数
df_uni.plot(kind='density',ax=ax_)

# 横軸の表示幅の設定
ax_.set_xlim(-0.2,1.2)
pass

_images/ccdf4e9716af80029436ab6f8b36c7819fc80b5250716744c90d85ee175d9b8c.png

多変量正規分布#

多変量正規分布に従うランダム変数の生成方法につて説明するが，例として２つの変数の場合を考える。変数の数が\(N>2\)の場合は，引数のmeanとcovを適宜変更すれば良い。

コード

rng.multivariate_normal(mean, cov, size=1)

mean：平均
- 2変数の平均ののリストもしくはarray
- 例１：[0,5]
- 例２：np.array([0,5])
cov：分散共分散行列
- 2次元のリストもしくはarray
- 例１：[[1,0.5],[0.5,1]]
- 例１：np.array([[1,0.5],[0.5,1]])
size：ランダム変数の組数（デフォルトは1）

ここで、.multivariate_normal()はrngのメソッドである。例として、平均は

mean = [0, 5]

共分散mは

m = 3

分散共分散は

cov = [[5, m],
       [m, 10]]

のランダム変数をn組

n = 5

生成しよう。

rng.multivariate_normal(mean, cov, size=n)

array([[-1.01380459,  5.67792347],
       [-1.34816096,  3.88873828],
       [-1.19041348,  9.47485894],
       [-2.68177605,  4.59411872],
       [-0.65032586,  9.3850437 ]])

各列がランダム変数の値を示しており，行が２つのランダム変数の１組ということになる。

２つのランダム変数を標準正規分布とするが，共分散はmのランダム変数を生成する場合もmeanとcovは省略できない。

mean = [0, 0]
m = 0.8
cov = [[1, m],
       [m, 1]]

rng.multivariate_normal(mean, cov, size=5)

array([[-0.83602116, -0.44301719],
       [ 0.5146715 , -0.04486816],
       [-0.67387514, -0.25662089],
       [-0.24472356,  0.68760672],
       [-0.43604238, -0.78825785]])

上の平均と分散共分散の２変量正規分布に従う1000個のランダムを生成し散布図をプロットしてみよう。

# ランダム変数の生成
vals = rng.multivariate_normal(mean, cov, size=1_000)

# DatFrameの作成，列ラベルをXとY
df_2norm = pd.DataFrame(vals, columns=['X','Y'])

# 散布図
df_2norm.plot('X', 'Y', kind='scatter', alpha=0.5)
pass

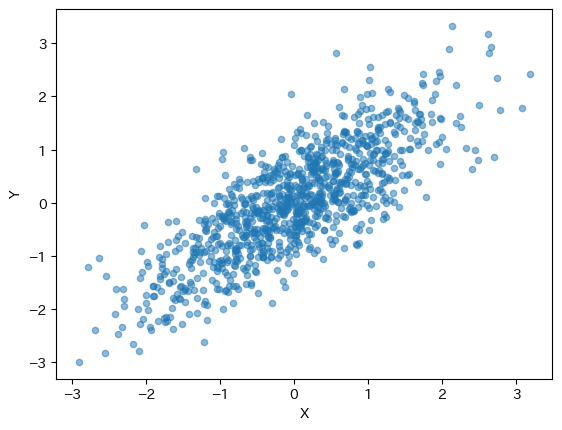
_images/bc2329a9a23a847527aedee5e55a8aed418f88ed08afeeafa56a0a79b756e50f.png

XとYの共分散はm=0.8となっているため，正の相関が観測される。相関係数を計算してみよう。

df_2norm.corr().iloc[0,1]

0.792327986719031

古い書き方#

上で説明したnp.random.default_rng()を使うコードが現在推奨されている書き方となるが，この書き方が導入される前の書き方を紹介する。現時点でも古い書き方を使うことができるが，ランダム変数の統計学的特徴という観点からは推奨されるコードの書き方の方が良いとされる。

コードの違いを説明するために，標準正規分布のランダム変数を１つ生成するコードを考えてみよう。 NumPyをインポートするコードも含めると，上では次のように書いた。

import numpy as np
rng = np.random.default_rng()
rng.normal()

最後の２行を１行にまとめて書くこともできる。

import numpy as np
np.random.default_rng().normal()

実際に実行してみよう。

np.random.default_rng().normal()

-0.44865932291647825

古い書き方では書き方では次のようになる。

import numpy as np
np.random.normal()

実際に実行してみよう。

np.random.normal()

0.6030325691718131

２つを比べると，推奨される書き方には.default_rng()が追加されていることが分かる。その部分が「より良い統計学的特徴」を発生させるコードとなる。

次の表にまとめることができる（インポートの行は省く）。

	推奨コード	古い書き方
平均1 標準偏差5の正規分布	np.random.default_rng().normal(1,5,size=10)	np.random.normal(1,5,size=10)
最小値1 最大値5の一様分布	np.random.default_rng().uniform(1,5,size=10)	np.random.uniform(1,5,size=10)
平均`mean` 分散共分散`cov`の多変量正規分布	np.random.default_rng().multivariate_normal(mean,cov,size=n)	np.random.multivariate_normal(mean,cov,size=n)

Numpy: ランダム変数

Contents

Numpy: ランダム変数#

はじめに#

ランダム変数生成コード#

正規分布#

一様分布#

多変量正規分布#

古い書き方#

`Numpy`: ランダム変数#